INTRODUCTION

   In this experiment, you will measure spring potential energy and gravitational potential energy, and show how energy is conserved.

EXPERIMENT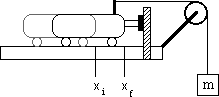

I. Determine the spring constant, k:

1. Check that the track is level; a cart placed on the track should not move.

2. Fully extend the spring plunger on the cart. Place the cart with the spring plunger against the end stop, as shown. Connect a string to the cart, and hang it over the pulley. Record the cart's initial position, x_i, in the table below.

3. Connect a mass hangar to the string, add additional mass (remember that the hangar has a mass of 0.050 kg), and record the new position of the cart, x_f. Calculate the cart's displacement, x from its starting position.

4. Repeat the above procedure for as many positions as possible (Note: the spring plunger might get "stuck", and prevent the spring from compressing further. Stop at this point).

5. Calculate the force exerted on the spring by this additional mass.

   Additional mass m (kg)	Initial position xi (m)	Final Position xf (m)	x = xf – xi (m)	F = mg (N)
   —	—	—	—	—

II. Measure Potential Energy:

1. Loosen the leveling legs on one side of the track (the side opposite the pulley), and slide them over toward the middle of the track.

2. Remove the string and mass hangar from the cart. Determine the mass of the cart, and record in the table below. Measure the distance that the spring plunger can be completely compressed into the cart. Return the cart to the track, this time with the plunger resting against the opposite end stop.

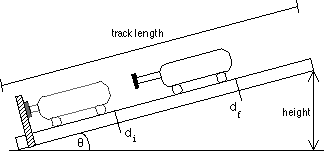
3. Incline the track until the angle gauge reads 10^o. (Note: you should still measure the height and length of the track, and calculate θ for your measurements). Record the angle in the table below.

4. Record the initial position of the cart with the spring plunger compressed, d_i.

5. Release the plunger by tapping it with a ruler; record the final position of the cart, d_f, and calculate the distance the cart traveled, d. Repeat this at least five times.

6. Record the maximum distance the cart traveled, d_max, and calculate the height the cart was raised, h.

7. Decrease the angle of the track to 5^o, and repeat your measurements.

8. Add mass to the cart (with the track at the lower angle), and repeat your measurements.

Track Angle θ	mcart (kg)	Initial position di (cm)	Final position df (cm)	d = df – di (cm)	dmax (cm)	h = dmaxsinθ (cm)
—	—	—	—	—	—	—

ANALYSIS

1. Hooke's Law states that the spring constant, k, is the proportionality constant between the force applied to a spring, and the amount that it compresses or stretches: F = kx. Use Excel to plot F vs. x, and calculate the spring constant.

2. The potential energy (PE) of a spring compressed a distance x from its equilibrium position is given by: PE = ¹/₂kx². Calculate the spring's potential energy from your measurement in step 2, part II.

3. The gravitational potential energy gained by the cart as it climbed the incline is calculate as: PE = m_cartgh, where h is the height the cart was raised. Calculate the gravitational potential energy for each case you measured.

4. If energy is conserved, the potential energy in the compressed spring will be completely converted into gravitational potential energy. Calculate the percent difference in you potential energy measurements, and see whether energy was conserved.

REPORT

• Create a table that summarizes your potential energy measurements, and their percent differences.
• Which of the potential energies was larger? Where did this "lost" potential energy go?
• When the mass of the cart was doubled, what happened with the gravitational potential energy? Why?

Return to Physics 103

©	St. Lawrence University	Department of Physics

Revised: 25 Aug 21

Canton, NY 13617