INTRODUCTION

   The purpose of this experiment is to measure the difference in temperature (ΔT) between a cup of cooling water and the room as a function of time. You will then see if the data are consistent with Newton's law of cooling, which predicts ΔT to be an exponential function of the elapsed time.

THEORY

   Newton suggested that the rate of heat flow from a hot body (that is, Q/Δt, where t represents time) is roughly proportional to the difference in temperature between the body's temperature (T_water, if that body is water) and the temperature of the surroundings, T_room. Since we often recognize heat flow by a temperature change (Q/Δt is related to T/Δt), Newton's law of cooling simply says that T/Δt = k(T_water - T_room), where k is a constant. Since T_room is constant, ΔT = (T_water - T_room) so we can write:

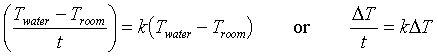
   Thus the rate at which (T_water - T_room) changes is proportional to (T_water - T_room). When a quantity varies in this way it is said to vary exponentially with time:

or

where T_o is the initial change in temperature, t is the elapsed time, and τ is called the time constant. τ is the amount of time for the temperature to "decay" to 37% of the original T_o.

EXPERIMENT

1. You have two thermometers, one for measuring the temperature of the water and one for measuring room temperature. A 10 milliliter beaker holding a small amount of hot water is placed in a plastic box to protect it from drafts. Although the thermometer is marked in whole degrees, try to read the temperature to the nearest 0.10°.

   Set up the following data table in your notebook. The elapsed time is the time that has passed since your first observation. Note that your first measurement occurs at t = 0!

   Elapsed time, t (min)	Twater (°C)	Troom (°C)	ΔT = Twater – Troom (°C)
   0.0	—	—	—
   0.5	—	—	—
   …	—	—	—
   20.0	—	—	—

2. Observe the temperature in the water and the room every 30 seconds for five minutes, then every minute for the next 15 minutes.

ANALYSIS

3. During other experiments that we perform this semester, we typically will graph points as the data is collected, to ensure that the experiment is behaving as expected. In this experiment, care must be taken during the data collection, so you won't be able to graph as you go along. After you have finished collecting your data, use Excel to create a graph of ΔT vs. t.

4. Fit an exponential curve to your Excel plot. From the equation Excel calculates, determine the time constant, τ.

REPORT

• State your value for the time constant. What are the units for τ?

• When this experiment has been performed in the past, it was noted that the data deviates from the (theoretical) exponential curve, especially during the first few readings. Does your data exhibit this behavior? Compare your graph to those from other groups. Do they show similar trends? What conclusions can you draw from this?

Return to Physics 103

©	St. Lawrence University	Department of Physics

Revised: 25 Aug 21

Canton, NY 13617