Newton's law applied to the oscillating spring-mass system gives the period, T, in terms of the spring constant and the total
suspended mass, M (be careful with the notation!):
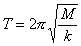 (Equation 1)
(Equation 1)
As usual, we wish to see if this theory accurately predicts the behavior of our experiment. However, for our experiment, we are using springs with a mass that is similar to the mass being suspended from it. The trouble is that an unknown fraction of the spring's mass, mu, also contributes to the oscillation period. So, the total suspended mass is actually:
M = m + mu
The result is that the entire graph gets shifted to the left by an amount equal to this unknown contribution of mass. Theory predicts that this unknown contribution is approximately one-third of the springs mass, mspring.
You will be using Excel for your analysis. Equation 1 is a power function, in the form of y = axn, where n is 0.5. Unfortunately, Excel will adjust n as well as a to get the best fit. If n is not 0.5, then the results will be lousy.
So, we will have to use the time-honored technique of linearizing the data. This was the method used to analyze non-linear experimental data before the advent of computers, when everything was done with nothing more sophisticated than a pencil and a ruler (imagine that!). It is difficult to determine quantities from a non-linear graph. However, if we can linearze the data (i.e. put it in the form of a straight line: y = (slope)x + b), then we can easily determine the desired quantities from the slope and y-intercept.
To speed up the analysis, you will use Excel to linearze the data. Using algebra, Equation 1 can be put in the form of a straight line (make sure you know how to do this):
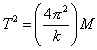 (Equation 2)
(Equation 2)
So, if you plot T2 vs. M, you would expect to get a straight line that goes through the origin (why will it go through the origin?). For our experiment, you will be plotting T2 vs. m, and will get a straight line that has been shifted to the left (because m = M – mu!). The absolute value of the x-intercept will give the unknown fraction of the spring mass, mu, that is included in the total suspended mass.
- Use Excel to create a table of your data: m and <T>. Add a third column for <T>2 (make sure you include column titles in your spreadsheet – you'll have to use <T>^2 for <T>2). You will use Excel to quickly calculate the value of <T>2 as follows:
- Click once in the blank cell below your <T>2 label. Type an equal sign, then click the cell next to it under the <T> column. This will place the "cell address" (e.g. B2) in the equation. Next, type a carrot (^), and then 2. The equation in the cell should appear as follows:
=B2^2
Press the Enter key to square the contents of cell B2.
- It would be time consuming to repeat this procedure for the entire column. Excel provides a quick method of copying the equation you just created, adjusting it to properly calculate the squares of the <T> column. Click once on the cell containing the equation you just created. You'll notice a little "handle" in the lower right corner of the hi-light of the cell. Move the cursor over the handle, and you'll see it turn into a small plus (+). Click and hold the left mouse button on this handle, then drag it down the appropriate length of the column. Release the mouse button, and you'll have calculated <T>2 for the entire column. Pretty cool, eh?
- You will next plot both sets of data on the same graph. Be sure to select the column titles when you drag over your data to begin the graph. In step 3 of the Chart Wizard (Chart Options), click the Legend tab, and turn on the option to display the legend. This way, you'll be able to distinguish between the two data sets.
Since you are plotting two different sets of data on the same graph, it's ok to leave the y-axis label blank (you should still label the x-axis appropriately). Also, in the last step of the Chart Wizard, choose As New Sheet for the graph location; it will print better, and be easier to analyze.
- Once you have your graph created, add a trendline for the linear data (you won't be able to add a trendline of the correct function – power – for the non-linear data!). Increase the backward forecast of the line 5 to 10 units, so that the line crosses the x-axis.
- The absolute value of the x-intercept is the unknown portion of the springs mass, mu, that affects the results of our experiment. You'll be able to read this value directly from the graph, but some modifications are required to make it easier.
- Double-click on the x-axis grid line (make sure you pick the x-axis, and not just any horizontal line!). In the dialog box that appears, turn on the minor tick marks (choose inside or cross), then click the Scale tab.
- Set the scale of the x-axis so that major units are 2, and minor units are 0.5, then click the OK button. This will place a number every two units along the x-axis, and smaller tick marks will appear every 0.5 units. You may need to customize these settings to suit your data; you should be able to easily read the value of the x-intercept.
- Add your names, print you graph, and determine the values of mu and k.
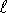 ) as the suspended mass, m, changed from 10 to 20 grams.
) as the suspended mass, m, changed from 10 to 20 grams.
![]() .
Hooke's Law states that there is a linear relationship between the change
in spring length (Δ
.
Hooke's Law states that there is a linear relationship between the change
in spring length (Δ![]() )
as the result of different forces (i.e. weight) pulling on the
spring (ΔF). k is the proportionality
constant between these two quantities.
)
as the result of different forces (i.e. weight) pulling on the
spring (ΔF). k is the proportionality
constant between these two quantities.
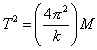 (Equation 2)
(Equation 2)