Phys 151 - Creating Graphs With Maple

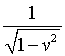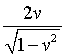
Creating Graphs With Maple

INTRODUCTION

Maple is a powerful symbolic computer language. This exercise is designed to introduce you to Maple's graphing capabilities in the context of the class work we are doing in special relativity.

Loading Maple

Open the SLU Network menu, and open the "Software for Courses", "Mathematics" folders. Double-click on the Maple V, release 5.00 icon.

Note: If you open an existing worksheet and need to make changes or additions, you must first select Edit => Execute => Worksheet.

Issuing Maple commands

The basic Maple document is a worksheet (like the document you are reading right now) which contains text, input, and output. To enter an input statement you must first have the prompt character displayed. When your Maple session starts, there will be a prompt (>) inserted automatically. Prompts can also be inserted from the menu bar. Here is an example of a Maple statement which assigns a value to a variable.
m:=2
Always use := for the assign statement, with no spaces between ":" and "=". Always end every statement with a semicolon. Note that Maple responds with an output line centered on the page. Also note that variables are case sensitive, so 'm' and 'M' would be recognized as distinct variables.
Maple can also be used as a calculator:
12
Let's define a function. Use the example of γ in special relativity. It's awkward to use certain Greek symbols in Maple (your instructor can tell you how to use some of them), so we'll use g instead:
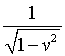
To plot g as a function of v for the domain [0,1], enter the following:
The graph will appear below your function (the color=black option will draw black lines; they are easier to see on the screen, and print better on a monochrome printer).
Now let's see how you can restrict the range of the function being plotted to lie between 0 and 5 (You can type the new line below, or edit the previous statement and re-execute it. Any statement can be re-executed by placing the cursor anywhere in the line and pressing the Enter key).
Notice how γ is practically equal to 1 for speeds less than 0.2.
More than one function can be plotted on the same graph. Try the following:
Note that each there are no line labels; it's up to you to know which function is associated with a particular line.

Comparing classical and relativistic formulas for momentum and kinetic energy

According to Newton, the equation for momentum is p = mv. In relativity it is modified (because time and length differ in different reference frames) to p = γmv. Let's define these functions in Maple and plot them. We have already defined γ in step 3, and have already assigned the mass to be 2. It is hard to use units in Maple, so we will assume standard (SR) units. This means that you will have to be sure to keep track of the units for yourself.
p:=2v
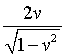
Plot these two functions on the same graph and see how they agree for small velocities (from v = 0 to 0.5)
Define a third function, pf, for the fractional difference (pr – p)/p, and add it to your plot, setting the range of v from 0 to 1.5. Use the instructions below to print this graph of p, pr, and pf.
The relativistic equation for kinetic energy is Kr = (γ – 1)m. Make a double function plot comparing Kr to the classical expression for kinetic energy for v = 0 to 1.2. Change the range on the scales to see where K and Kr begin to diverge. Discuss these results, and print the graph.

Printing Graphs

To print a graph, click on it once to select it, and choose Copy from the Edit menu. Choose New from the File menu, and then choose Paste from the Edit menu. You can then choose Print from the File menu to print the graph (if you don't follow this procedure, you'll print your entire document!).

REPORT

Hand in your graphs from steps 9 and 11. On the graph, label each function, and write a brief description of its significance.

Return to Physics 151


©	St. Lawrence University	Department of Physics