INTRODUCTION

    For the purpose of this experiment, assume that there exists an ether that permeates all space and is at rest, and that light travels with a speed of c in that ether. The ether is fixed in space, so if we travel with some speed through the ether, then the speed of light we measure would be given by the Galilean velocity transformation,

V' = C ± β

depending upon whether we are moving in the same direction as the light wave, or opposite to it.

    If light is a wave in the ether, then we can characterize a light beam in the same way we did other waves in Unit N (see chapter N12.3 in Moore). For our purposes today, the most useful characteristic of a light wave will be its period T, the time for a wave to complete one cycle.

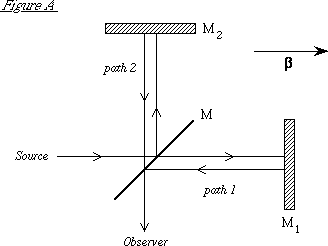
    The Michelson interferometer (figure A) was designed to test this assumption. It splits a beam of light into two beams by a partially reflecting surface; the two beams travel along perpendicular paths and are then reunited to form an interference pattern; this pattern is sensitive to any differences in the speeds of the light traveling along the two paths.

    We can find the difference in the time of travel for the two beams of light in the following way: assume path 1 is exactly parallel to the earth's velocity β. In this case the light travels from M to M₁ with speed c + β (relative to the interferometer) and back from M₁ to M with speed c – β. Thus the total time for the round trip on path 1 is:

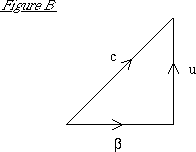
    The speed of light traveling from M to M₂ is given by the velocity-addition diagram in figure B. That is, relative to the earth, the light has velocity u perpendicular to β; relative to the ether it travels with speed c in the direction shown. This speed is

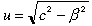
    Since the speed is the same on the return journey, the total time for the round trip on path 2 is

    Comparing t₁ and t₂ we see that the waves traveling along the two paths take slightly different times to return to M (which takes longer?), the difference being

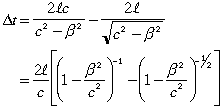
    By the binomial approximation, we can write this as

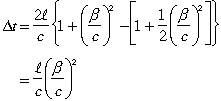
    If this difference Δt were zero, the two waves would arrive in step and interfere constructively, giving a bright resultant signal. Similarly, if Δt were equal to half a period of the light wave, the two waves would be exactly out of step and would interfere destructively. We can express the number of complete cycles by which the two waves arrive out of step in the following way:

    If we were to then rotate the interferometer 90^o, as Michelson did, this difference should double from one position to the next (why?):

    Michelson believed that it should be possible to detect a shift of this much with his interferometer, allowing him to show that light travels at different speeds in different directions.

EXPERIMENT

Part I

1. Familiarize yourself with the operation of the low-tech interferometer and sketch it in your lab report. Be sure to include dimensions.

2. We are using a mercury light with a green filter on it as a light source. This ensures that the light you look at in the interferometer all has about the same wavelength and period, T. The period of this light it T = 1.8 x 10^–15 s.

3. Adjust M₁ until you can find an interference pattern when you look toward M. At the center of a symmetrical pattern you will see what looks like a bulls eye. Try to get the pattern as close to this as possible.

4. Assume the earth is moving through the fixed ether to the east with a speed of approximately 3 x 10⁴ m/s (the earth's orbital velocity around the sun). Align your interferometer so that one arm is parallel to the direction of β and one is perpendicular. From the values of T for the light, β, and the dimensions of the interferometer, calculate how much time difference you should see for the two paths of light. What fraction of a period is this?

5. Now rotate your interferometer by 90^o and sketch the new orientation with respect to the ether. Calculate the expected time difference for this case.

6. What total shift in the interference pattern (ΔN) should you expect to see with this interferometer if our hypothesis about the speed of light were true?

Part II

7. You are now ready to try using the higher-tech Michelson interferometer. This one uses a laser light source with a period of T = 2.2 x 10^–15 s. Your instructor will show you how to operate this interferometer. From measurements of the lengths of the two arms, calculate how much of a period the pattern should shift when you rotate the interferometer by 90^o.

DISCUSSION

• Summarize your conclusions from Parts I and II. Michelson expected to see a difference in the interference patterns for the two orientations of the interferometer, which would have told him that light traveled at different speeds in different directions. Assuming that his original assumption were correct, do you thing this shift should be observable with either of the interferometers you used here? Explain your answer completely.

Return to Physics 151

©	St. Lawrence University	Department of Physics

Revised: 25 Aug 2021

Canton, NY 13617