Phys 151 - The Square Pendulum

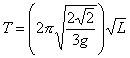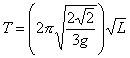
The Square Pendulum

PURPOSE

You will test to see how precisely the period (T) of a real pendulum is related to its size (L) by Newton's prediction: T = kLⁿ.

INTRODUCTION

A physical pendulum consists of any rigid object that is hung from a pivot point and allowed to swing. Today we will work with squares of various lengths (L), suspended by one corner.

The period of a pendulum is the time for one complete swing, over and back. The amplitude of pendulum motion is the angle measured from the equilibrium position in the middle to the farthest point on either side.

The expression T = kLⁿ implies that the period (T) of a pendulum depends on its size (L), and shape (k) where, for today, k can be calculated from the geometry of a square. Newton's law will give a value for n.

Our expression neglects the weak dependence of the period on the amplitude. Since T increased about 1% at 10^o, we will succeed if we keep the amplitude as small as possible.

PROCEDURE

The pendulum is a square metal plate pivoted at one corner. Since the axle is delicate, always rest the squares so that the axles are off the table and off each other (otherwise you may well learn how to solder!). You want to find the relationship between the period of such a pendulum and one of its dimensions. We suggest that you measure the length of the side of the square, but you may measure another dimension if you choose. Confirm that each pendulum is indeed square and that they differ only in the length of a side.
Start a data table that includes the units and definition (in a sketch) for each table heading.
Put your photogate timer in "pend" mode, and the "0.1 ms" setting. Measure the pendulum's period, using small amplitude swings. Make sure the light on the photogate blinks twice for each swing.
To begin the graph of period vs. length of side, you will need to set the axes scales; use the largest pendulum to get the biggest T, and the origin (0,0) to scale the axes.
Repeat measurements for other sizes, plotting as you go, until you are satisfied that your graph has enough points on a smooth curve.

ANALYSIS

Use Excel to plot your data and find the parameters k and n for the best-fit line. The function for a pendulum is:

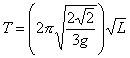
Find the expected k and n from this expression.

DISCUSSION

Begin with the numerical results (best k and n, and the expected k, n) and a reference to the graph.
Discuss whether or not the data are consistent with each other (are they on a reasonably smooth line?) and with the theory (could your points belong to the computer curve?).
Discuss whether you think your values could equal the expected values.

PROJECT

Have your instructor give you a pendulum that you have not previously tested. Predict its period from your values of k and n. Hedge your bets by quoting an uncertainty. Measure the period directly, and add the data and conclusion to your lab report.

Return to Physics 151


©	St. Lawrence University	Department of Physics