- Computers are needed for lab this week
- Students will come up with a 'model equation' that they can use to predict the period of an "unknown" square pendulum
- I seem to have run out of blackboard space, but here is a list of common mistakes that students are still making on their lab journals. If I'm smart, I'll make copies of this list to hand out. Please go over these points:
- Lab journals: What are you still forgetting?
- Read. The. Directions!
- Description/explanation: What are you doing?
- Which track did you use? Label on sketch
- Lengths with metersticks: Difference between two measurements
- Is {0,0} on the graph? Must be in data table
- Need more than one measurement for object in motion
- Units! Sig. figs!
- Solve problems algebraically first
- Use appropriate labels for model equations (e.g. y and t, not x and y)
- Measurement instrument used? Settings?
- Be sure to emphasize the fact that the pins are fragile, and should always be placed with the pin hanging over the edge of the bench. And don't be surprised when they ignore you!
- The pendula used for their data are on the side table (near the front lab entrance door), grouped by size. There are only seven groups of pendula, so everyone's graph will have 7 points
- Pendula are labeled by size (A-1, B-3, etc.); students should be encouraged to record which pendulum was used, so that can use the same one to double-check results
- {0,0} is not included as a data point this week
- They only need to use one unknown pendulum to test their model. They are arranged on the instructor's bench
- The correct model follows a power law (it's a square-root function); a second-order polynomial will produce a "close" model; be sure to ask students who choose a quadratic if their model makes sense ("What period does your graph predict for a pendulum of zero length?"). Note that they should follow the instructions and make the origin visible on their graph, or else they will pick the wrong model!
- Model: T = a·Lb
- b is unit-less (you should tell students this after they have chosen the correct function!)
- The actual units of parameter a are
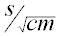 , but students will get , but students will get 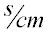 since they won't figure out that the function is actually a square root since they won't figure out that the function is actually a square root
- A former student – who had an aversion to learning new concepts – asked why the uncertainty had to be calculated using the RMS residual, and not just the min and max values of a and b. I set up a spreadsheet (Why-RMS-Residual) calculating the uncertainty both ways. Using the RMS residual, the difference between the predicted min and max periods is only 1%; that range increases to 2% when using the min and max values of a and b. I can supply you with the Excel file if you're really interested
- Check that students have the length of their pendulums as the difference between two readings on the meter stick. This is the third experiment this semester where they should be following this procedure, and they will follow it again on at least two more experiments
- My physical measurements of pendulum length. All lengths are ±0.2 cm:
- Experimental pendulum lengths (cm):
- A: 40.6
- B: 27.9
- C: 21.7
- D: 17.7
- E: 14.6
- F: 8.9
- G: 6.2
- Unknown pendulum lengths (cm):
- A: 13.1
- B: 18.7 x 18.9
- C: 9.2
- D: 19.6
- F: 12.0 x 12.1
- G: 11.0 x 11.1
|
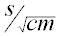 , but students will get
, but students will get 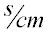 since they won't figure out that the function is actually a square root
since they won't figure out that the function is actually a square root