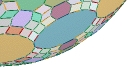
The 61-Zonohedron

This complicated spherical object is the largest convex polyhedron that can be built using standard Zome tools, a remarkable set of three-dimensional mathematical construction pieces. Zome tools consist of white balls, or nodes, into which blue, yellow, red, and green struts may be fitted. Given a fixed orientation of a node, it is possible to insert the various struts in a total of 122 different ways, along 61 different lines, or zones. In the construction below each direction is utilized the maximum possible number of times. Although it would be impractical to perform the actual construction of a 61-zonohderon, since it would only collapse under its own weight, it is possible to create a virtual model of this remarkable object using Scott Vorthmann's vZome software, which was used to render the picture below. The faces are paneled in and shaded to better illustrate the symmetry of the object. Zome tools motivate a number of interesting mathematical questions, several of which are posed below the model.

1. The 61-zonohedron has quite a few axes of symmetry. Identify the 2-fold, 3-fold, and 5-fold axes of symmetry. (Taken together these rotations form the icosahedral group.)

2. Although more than half of the surface of the polyhedron is hidden from view, it is possible to accurately count the number of struts needed to build the model. What is the shortcut?

3. Using the technique alluded to in the previous question, count the total number of vertices V, edges E, and faces F on this polyhedron. As a check confirm that V+F=E+2, a relationship called Euler's formula that holds for any convex polyhedron.

Please contact Professor Vandervelde if you wish to confirm your answers to any of these problems.