CS 256 - Exam 2 Study Guide

Exam 2 is everything starting from Day 10 on the course web site.

1. Stacks. Review the stack data structure, expression evaluation, and the assigned self check exercises. (Day 10 and 11)
2. Review the Queue data structure and the assign self check exercies. (Day 12 and 13)
3. Recursion: Study the examples we wrote in class and also those from the recursion study guide (Day 14)
4. Binary Trees and Binary Search Trees. Review all of the code we devloped for these. Know how to insert, find, and delete a node in a binary search tree. More questions below.
5. Do the tree study questions previously assigned.
6. Review Quiz 2

Binary Search Trees

1. Name five examples where a tree data structure (not necessarily binary tree or binary search tree) would be useful in practice.

   Five examples might include representing a 1) directory structure, 2) a family tree, 3) an HTML document, 4) arithmetic expressions, 5) data with an ordering (a binary search tree)

2. Name an example use of a binary tree (not binary search tree)

   An expression tree

3. When is a binary search tree appropriate?

   If we have data that should be ordered on some key value (i.e., last name, SSN, etc.) so we have fast access, inserts and deletes.

4. Essay question. Write a short essay that compares and contrasts the Binary Search algorithm with a Binary Search Tree. Address the positives and negatives of each. Make sure to address space and time efficiency. (Half a page)

   We talked extensively in class about this.

5. Write a recursive find method for a binary search tree.

   	public E find(E data) {
   	  return find(data, root);	
   	}
   	
   	private E find(E data, Node<E> root) {
   	  if (data.compareTo(root.data) < 0)
   	    return find(data, root.left);
   	  else if (data.compareTo(root.data) > 0)
   	    return find(data, root.right);
   	  else
   	    return data;
   	}
   

6. Draw the binary search tree that results from inserting the numbers below starting with 70 and ending with 62.

       70 11 47 81 20 61 10 12 13 62
     

   
7. For the tree above list the nodes in a preorder traversal.

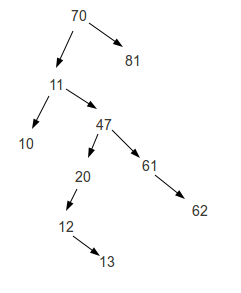
         70, 11, 10, 47, 20, 12, 13, 61, 62, 81
       

8. For the tree above list the nodes in a postorder traversal.

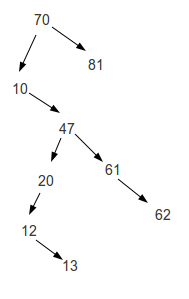
         10, 13, 12, 20, 62, 61, 47, 11, 81, 70
       

9. For the tree above list the nodes in an inorder traversal.

         10, 12, 12, 13, 20, 47, 61, 62, 70, 81  
       

10. What did you notice about the inorder traversal of a binary search tree?

    It is in increasing order.

11. Redraw tree after deleting 11.
    
12. Write a recursive function size that returns the number of nodes in a binary tree.

    public int size() {
      return size(root);
    }
    	
    private int size(Node<E> root) {
      if (root == null)
        return 0;
      else
        return 1 + size(root.left) + size(root.right);
    }
        

13. Given our definition of a binary search tree, what does the following binary search tree method do on a non-empty binary search tree?

      public E mystery() {
          Node curr = root;
          while (curr.right != null)
             curr = curr.right;
          return curr.data;
      }
    

    This returns the largest node in the tree by going all the way to the right.

14. Give a precondition for the binary search tree mystery method above (other than the obvious that root must refer to a binary search tree).

    The tree should not be empty otherwise curr.right results in a null reference exception.

15. Write the find method for our BinarySearchTree class binary search not using recursion but using a loop.

    public E iterative_find(E data) {
        Node curr = root;
        if (curr == null) 
          return null;
              
        while (curr != null)
          if (data.compareTo(curr.data) < 0)
            curr = curr.left;
          else if (data.compareTo(curr.data) > 0)
            curr = curr.right;
          else
            return curr.data;
    
        return null;
    }
    

16. What is the height of the "shortest" binary search tree that has 403 nodes.

    Here's a few ways to think about. You could just apply the formula and get $log_2(403)=8.65$. Since height must be integral the the height must be 9.

    The other way to think about it is that a tree of height 1 has at most 1 node, 2 has at most three nodes, 3 has at most 7 nodes, $n$ has at most $2^n-1$ nodes. So a tree of height 8 has at most 256 nodes. Then 9 has at most 512 nodes. And 403 is between 256 and 512 so it miust be 9.

17. What is the height of the "tallest" binary search tree that has 403 nodes.

    That would be a degenerate tree and it would have height 403.